

First, there is the probability that you will draw a fair coin and then there is the probability of the coin landing on heads. If you think about the problem there are two probability steps. The exercise questions ask you to tell the combined probability of a series of coin flips, where the coin to be flipped could be fair or not. Yikes! That explanation got kinda long! I hope it helped :-) Then, all he had to do was figure out how many 9-card hands he could have based on that assumption. This is essentially the same thing Sal did, but instead of assuming he had just one card in his hand at the outset, he assumed he had all four 1s.
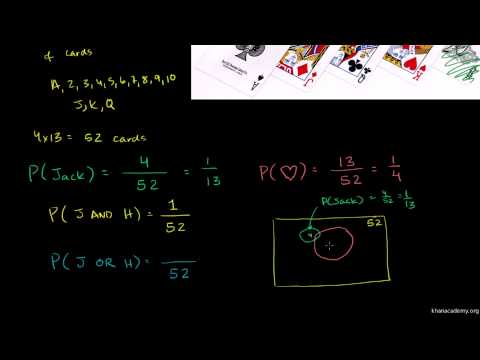
Then, just divide this by the total number of possible hands and you have your answer. This would tell you the total number of hands you could have (52 minus the four of hearts = 51). Using a standard deck of cards, what would the probability be of having the four of hearts in your 2-card hand? Well, you can start by assuming you have the four of hearts, then figure out how many options you would have for the other card in your hand. We can essentially ignore the four 1s because we already accounted for them by assuming we had them from the outset.Ī simpler example might examined a 2-card hand (perhaps we're playing blackjack or something). The question then became how to fill the other five "slots" in our hand, which turns out to be (32*31*30*29*28)/(5!). Sal took this idea (the idea that there is only one way way to have all of the ones if our hand only had four cards), and he built from there. Unfortunately, we have 5 other cards in our hand as well, which make this more complicated (and interesting). If the size of our hand were just four cards, there would be exactly one way to do this. We know our hand will have four 1s in it.


 0 kommentar(er)
0 kommentar(er)
